Brief Description
This activity uses a simple analogue for the power of radiation received at a given distance from a star. A photovoltaic cell is connected to an electric motor. Depending on the power received on the cell, the motor begins to move. It changes also its speed with respect to the distance between the cell and the lamp. This can be interpreted as a model for a planetary system and its habitable zone. The “engine of life” moves, as soon as the receiving power is big enough to sustain its operation. The distance, where the motor stops, can be interpreted as the outer edge of the habitable zone.
This resource is part of the educational kit "The Climate Box". You can read more about the kit in the presentation attached. Find all related resources selecting the category "Our fragile planet" and "secondary level".
Goals
With this model experiment the pupils
- understand the qualitative correlation between the distance of a planet to a star and the energy density that impacts the planet.
- learn that liquid water in a planetary system can only be present in a confined corridor, the habitable zone.
- understand that searching for extra-terrestrial life as we know it means to look for conditions to keep water liquid.
- understand that the size and extent of a habitable zone depends on the luminosity of a star.
Learning Objectives
The pupils are supposed to carry out or observe a simple model analogue experiment that represents the nature of a habitable zone around a star. They have to follow the instructions provided with the description and measure distances with varying boundary conditions. Finally, they have to analyse and interpret the result as well as discuss the relation to planetary systems and habitable zones in general.
Evaluation
The pupils should be able to explain the phenomenon observed in their own wording. They should also be able to record and analyse data on their own and draw the necessary conclusions for their environment. With support they should be able to explain their observations correctly. In case the necessary physical basic concepts have not been reviewed yet the pupils should be able to explain their observations in their own wording.
Question 1: Is there life on Mars?
We haven’t found anything that would point towards that direction.
Question 2: Is there liquid water on Mars?
Very little to none. At least not so much that we can expect sustained open water areas or running rivers.
Question 3: Why are those two things related?
Water is the key to life. Without water, there is no life the way we know it.
Question 4: What does it take to support life on other planets?
There are a few conditions that help sparking and sustaining life, but the key is – again – water. Heat is only needed to keep the water liquid, at least in some places. Other boundary conditions that may help are energy sources (light, chemical) or magnetic fields to fend off ionising particle radiation. But as long life evolves in oceans, this does not really matter.
Question 5: What conditions are needed to keep water liquid?
Heat, and perhaps salt. Salt helps to permit lower temperatures to keep water liquid.
Question 6: What provides us and other planets with the heat needed to keep water liquid?
Stars, the Sun. A greenhouse effect provided by an atmosphere helps to raise temperatures.
Question 7: What happens to water, if it is very cold or very hot?
It freezes or boils and evaporates.
Question 8: How will the motor behave, if the cell is held at different distance from the lamp?
The rotation speed depends on the distance. Far = slow, near = fast.
Tasks:
- The distance necessary for the electric motor to begin to move is smaller with a dimmed lamp than with a bright lamp.
- A planet in a planetary system with a star that less bright than the Sun needs to be located closer to then sun in order to be in the habitable zone.
- It runs very fast. It “overheats”.
- No, because with decreasing distance the receiving power rises. This leads to an increased heating of the planet. If the temperature is too high, water cannot remain liquid.
Materials
Since photovoltaic cells are quite expensive, teachers may prepare a restricted number of experimental set-ups. The experiment needs the following items.
- Strong lamp, floodlight
- Dimmer to regulate the brightness
- Folding rule or yardstick
- Photovoltaic cell with attached electric motor (be sure that the power the cell generates is big enough to drive the motor)
Background Information
The Circumstellar Habitable Zone
The most important ingredient to sustain life as we know it is liquid water. Therefore, if scientists want to find planets of other celestial bodies, where life may be present, they first want to know, if water exists in liquid form there. This, for instance, is also one of the major goals when exploring and investigating Mars.
The presence of liquid water depends on environmental conditions like air temperature and atmospheric pressure. The main driver of the surface temperatures of planets is their distance from the central star they orbit. Only in a small window the temperatures are just right so that water does not completely evaporate or freeze. These conditions are modified by local influences like the density of the atmosphere and the composition with potential greenhouse gases. This defines a range around a given star, in which liquid water could be present. This range is defined as the habitable zone. If a planet is found orbiting in this zone, it may potentially possess water in its liquid form and thus sustain life as we know it.
Planets that orbit stars other than the Sun are called extrasolar planets or short exoplanets.
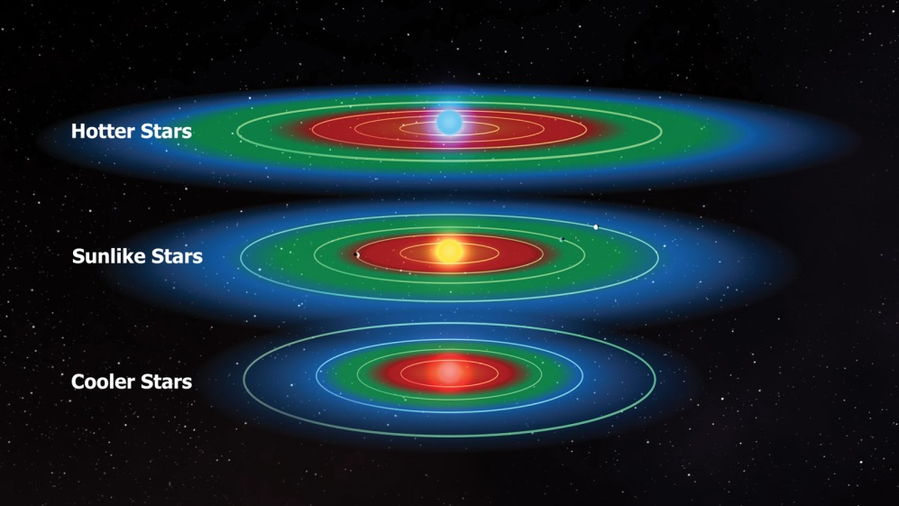
Figure 1: The circumstellar habitable zones of three stars that differ in size, luminosity and surface temperature (Credit: NASA/Kepler Mission/D. Berry).
Figure 1 shows the circumstellar habitable zone (in green) for stars of different temperature. The star in the middle corresponds to stars similar to the Sun. Hotter stars usually have a larger and wider habitable zone, while cooler stars can only provide smaller and narrower habitable zones. The blue area indicates that it is too cold for existence and the red area indicates that it is too hot.

Figure 2: Habitable zone (green) around the star HD 33793. The orbit of the extrasolar planet Kapteyn b is indicated (Credit: PHL/UCP Arecibo, http://phl.upr.edu/press-releases/kapteyn, https://creativecommons.org/licenses/by-nc-sa/3.0/legalcode, based on: Anglada-Escudé et al. 2014, MNRAS, 443, L89).
Figure 2 shows an example of an exoplanet around the star HD 33793, also known as Kapteyn’s star. The star has surface temperature of about 3570 K. This is about half of the surface temperature of the Sun with 5778 K. Thus, the habitable zone (indicated in green) is located at a distance between 0.11 AU and 0.22 AU.
Due to the lower luminosity, the habitable zone is closer to the star and narrower. When comparing the habitable zones of the Sun and HD 33793 (Figure 3), we find that they both differ considerably. The solar habitable zone is both wider and farther away from the Sun.

Figure 3: Comparison of the habitable zones (green) of the star HD 33793 and the Sun. (Credit: PHL/UCP Arecibo, http://phl.upr.edu/press-releases/kapteyn, https://creativecommons.org/licenses/by-nc-sa/3.0/legalcode, based on: Anglada-Escudé et al. 2014, MNRAS, 443, L89).
The exoplanet Kapteyn b with a mass of about 5 earth masses is located well within the habitable zone and therefore is interesting for further research on habitability.
Thermic radiation of bodies
Any given body with a temperature above absolute zero, i.e. T>0 K radiates. According to Planck’s Radiation Law (ideally for a black body) the distribution of frequencies of the emitted spectrum depends on the temperature.

Integrating over all frequencies leads to the Radiation Law of Stefan Boltzmann which describes the total emitted power. In reality black bodies only exist up to a certain degree of approximation. Therefore, Kirchhoff’s Radiation Law about the radiant power of any given body can be applied:

This means that the radiant power LΩν(β,φ,ν,T) of a given body is as large as the total radiant power of a black body LoΩ,ν (ν,T) having the same temperature and the same absorptivity aν'(β,φ,ν,T). The spectral radiance and the absorptivity may also depend on the angle of incident radiation. Thus, according to Kirchhoff’s Radiation Law, the radiant power of any given body is directly proportional to the radiant power of a black body with the same temperature. Furthermore, Kirchhoff’s Radiation Law leads to the conclusion that with a given temperature a body with good heat absorption also releases heat well.
Stefan Boltzmann’s Law
The Stefan Boltzmann’s Law describes the emitted power of a black body radiating isotropically into all directions. For the total radiation power of a black body the following equation applies:

A is the area of the radiating cross section of the body and σ is the Stefan Boltzmann’s constant, a natural constant with the value of:

Together with Kirchhoff’s Radiation Law the Stefan Boltzmann’s Radiation Law for any given body results to

with a temperature dependent emissivity ε(T).
The emissivity is a parameter that reflects the properties of the radiating substance and surface. For am given temperature, surfaces with different emissivity appear differently bright. As a result, the thermic radiation is also stronger.

Figure 4: Photographs of Leslie's cube. The color photographs are taken using an infrared camera; the black and white photographs underneath are taken with an ordinary camera. All faces of the cube are at the same temperature of about 55°C. The face of the cube that has been painted has a large emissivity, which is indicated by the reddish color in the infrared photograph. The polished face of the aluminum cube has a low emissivity indicated by the blue color, and the reflected image of the warm hand is clear (Credit: Pieter Kuiper; https://commons.wikimedia.org/wiki/File:LesliesCube.png, licence: public domain).
Radiation balance
A body that absorbs energy in form of thermic radiation warms up as long as the energy emitted is as high as the energy that is absorbed. This means that body is in thermal equilibrium. This scenario can applied to the Earth that receives electromagnetic radiation of the Sun with a flux density (solar constant) of:

If the Earth is in thermal equilibrium, the energy emitted must be as high as the energy absorbed. It is important that only half of the earth is irradiated at the same time. As part of the sunlight hits the surface in an angle not perpendicular, only an area as big as the cross section of the Earth is illuminated. Thus, the energy absorbed by the Earth is:

The energy emitted by the Earth can be calculated with Stefan Boltzmann’s law. Here it is important that the complete surface radiates.

With this, the temperature can be calculated, if the Earth did not have an atmosphere.

Simple model for circumstellar habitable zone
In the following, a simple model for characterising the circumstellar habitable zone has to be found. It is purely based on the assumption of thermal equilibrium. The total radiative power emitted by the Sun (luminosity) is derived from the solar constant, the surface of a sphere and the distance between the Sun and the Earth. Since the sun radiates in all directions isotropically, we can assume that the solar constant is valid for any point on such a sphere. We find:

The solar constant for any given distance r is:

This demonstrates that – as expected – the received flux density of a constant radiation source depends on the inverse square of the distance. Following the applied logic of the thermal equilibrium the effective temperature of a planet with the radius r_p results to:


With the constant

which for the Sun yields:

By selecting realistic limitations for the average temperature of a planet, the limits for a circumstellar habitable zone can be determined.
Full Activity Description
A key component of sustaining life on a planet is its capability of providing liquid water. For this, it is important that the receiving radiative power of the central star is big enough to raise the temperatures on the planet above a value that at least partially permits water to be liquid. This constellation can be seen as an engine of life that needs enough power to start.
Introduce the topic by asking about the solar system (planets, composition) and where in that system life had evolved. Perhaps, spark a discussion about the conditions of sustaining life on planets different than Earth (e.g. Venus, Mars). Try to direct the discussion towards the presence of water.
Question 1: Is there life on Mars?
Question 2: Is there liquid water on Mars?
Question 3: Why are those two things related?
Ask the pupils, if they have heard about planets around stars other than the sun.
Question 4: What does it take to support life on other planets?
Question 5: What conditions are needed to keep water liquid?
Question 6: What provides us and other planets with the heat needed to keep water liquid?
Question 7: What happens to water, if it is very cold or very hot?
The following experiment is a simple analogue, in which the star is represented by a lamp and the photovoltaic cell combined with the motor stands for the planet.
Experimental set-up
- Solder the motor to the photovoltaic cell.
- A coloured disc made of cardboard attached to the rotation axis improves the observation.
- Plug the lamp into the dimmer and then the dimmer into the socket.

Figure 5: Experimental set-up.
Question 8: How will the motor behave, if the cell is held at different distance from the lamp?
Experimental procedure
- Switch on the lamp.
- Hold the photovoltaic cell at a large distance from the lamp. The motor should not move.
- Approach the lamp and measure the distance at which the electric motor starts moving.
- Repeat this procedure for different brightness settings of the lamp by using the dimmer.
Tasks
- Write down your observations. Describe the results you get when varying the brightness of the lamp.
- Transferring this model experiment to the configuration of the solar system, life sustaining conditions (running motor) are possible, because the Earth (photovoltaic cell) is close enough to the Sun (lamp). It is the outer edge of the habitable zone. What does the experiment tell us about exoplanets in other planetary systems that are supposed to harbour life?
For term 7 and higher:
- What happens to the motor, if the cell is very close to the lamp?
- Can we expect planets sustaining life to be at any distance inside the outer edge of the habitable zone?
Curriculum
Space Awareness curricula topics (EU and South Africa)
Our fragile planet, Habitability
Conclusion
The activity teaches about habitable zones of planetary systems. It comprises a simple experiment that demonstrates how the flux density received by a body depends on its distance from the source. It consists of a strong lamp, a photovoltaic cell that receives its power from the lamp and drives a motor as soon as the power is sufficiently high. This is relevant for understanding the dimensions of a habitable zone, where liquid water can be present for certain boundary conditions. The running motor in the experiment depicts the running engine of life within a planetary system.

This resource was developed by Marco Türk, Heidelberg University with important contributions by Markus Nielbock, Haus der Astronomie, Heidelberg, Germany. This resource is under peer-review, proof reading, and will be updated and improved in the coming year.

